本篇文章给大家谈谈如何判断函数可导,以及大家最关心如何判断函数可导的问题,希望对各位有帮忙 , 不要忘记收藏本站 。
怎样证明一个函数在某一点是否可导?1.先求出这个函数f(x)在x0这一点的左导数 2.再求出这个函数f(x)在x0这一点的右导数 3.如果这两个导数值相等,那么就证明了这个函数在这一点可导,否则就不可导 。1 。
怎么判断函数的连续性和可导性?一个函数在某一区间上连续(可导)指的是该函数在此区间的任意一点上连续(可导) 。至于判断在某一点上函数是否连续或可导,即判断某个极限是否存在 。判断函数 。
判断函数可导不可导一共有几种办法?函数可导定义:(1)设f(x)在x0及其附近有定义,则当a趋向于0时,若 [f(x0+a)函数的条件是在定义域内,必须是连续的.可导函数都是连续的,但是连续函数不一定是可导函数.例如,y=|x|,在x=0上不可导.即使这个函数是连续的,但是lim(x趋向0+)y 。
z怎么判断函数的可导性?【如何判断函数可导】根据导函数的定义或者利用左极限等于右极限,这两个方法都可以,但更多倾向于第二个方法 x=0的左右极限相等即可, 即lim( x→0+)= lim(x→0函数是否可导例题如:y=X2一1,y'=2X 函数是否可导例题如:y=X2一1,y'=2X
怎样确定一个函数是否可导?没有具体的公式,对一般的函数而言,在某一点出不可导有两种情况 。1,函数图象在这一点的倾斜角是90度 。2,该函数是分段函数,在这一点处左导数不等于右导数 。。
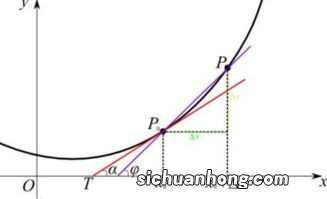
证明可导性的步骤?设函数y=f(x),定义域为M,证明函数f(x)在某点a(a∈M)可导的步骤: 1.给自变x的增量△x 。2.求函数f(x)的增量△y=f(a+△x 。设函数y=f(x),定义域为M,证明函数f( 。
可导性的判断方法和技巧?一个函数在某一区间上连续(可导)指的是该函数在此区间的任意一点上连续(可导) 。至于判断在某一点上函数是否连续或可导,即判断某个极限是否存在 。判断函 。
