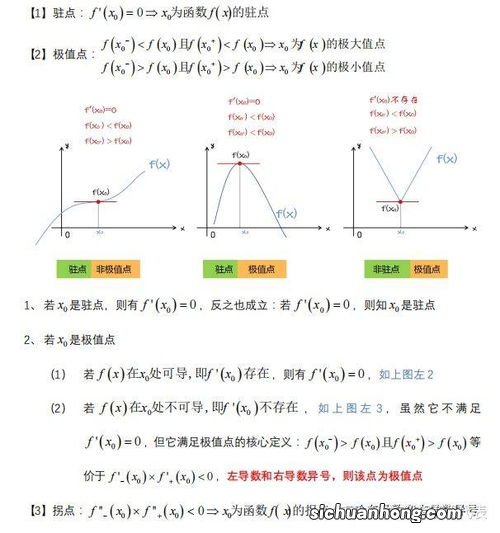
极值点是函数图像的某段子区间内上极大值或者极小值点的横坐标 。若f(a)是函数f(x)的极值,则称a为函数f(x)取得极值时x轴对应的极值点 。驻点关注的是,一阶导数的值为0 , 不关注函数的单调性变化 。驻点也是使函数凹凸性改变的点,而极值点是函数单调性发生变化的点,从单调递增变成单调递减的点是极大值点,从单调递减变成单调递增的点是极小值点 。
如果极值点是可导的点,那么一阶导数一定为0,即可导的极值点一定是驻点 。但是极值点完全可以是不可导的点,比方说y=|x|,这个函数 , 在x=0点处,函数从从单调递减变成单调递增,是极小值点,但是这个函数在x=0点处不可导,左右导数不相等 。不是驻点 。所以两者的区别是,驻点不一定是极值点,极值点也不一定是驻点 。以上就是驻点和极值点的区别的内容,下面小编又整理了网友对驻点和极值点的区别相关的问题解答,希望可以帮到你 。
请问函数的驻点和极值点的区别?函数的驻点:函数导数为0的点称为函数的驻点; 函数的极值点:是在这点附近这一点所对应的函数值最大或者最小(注意是这个点附近). 存在极值点的情况有两类,一类 。
极值点、驻点、拐点的区别?函数的导数为0的点称为函数的驻点,驻点可以划分函数的 。(驻点也称为稳定点,临界点 。) 驻点和拐点的区别 在驻点处的单调性可能改变,在拐点处单调性也可能 。
极值点、拐点、驻点的表示方法的区别?函数的导数为0的点称为函数的驻点,驻点可以划分函数的 。(驻点也称为稳定点,临界点 。) 驻点和拐点的区别 在驻点处的单调性可能改变,在拐点处单调性也可能发 。
驻点和极值点的区别?区别如下: 1、定义不同 。极值点:若一个函数的某一点存在某一邻域,在该邻域内函数处处都有定义,而该点的函数值为最大(小),则该函数在该点处的值就是一个极 。
极大值点和驻点的区别?首先,极大值点不一定是驻点 。如果函数y=f(x)在区间[a,b]上是单调的,那么函数y=f(x)在区间[a,b]上的极大值点就是区间的端点 。此时,区间的端点处的导数值未必 。
临界点、驻点、拐点的定义是什么?函数的一阶导数为0的点称为函数的驻点,驻点可以划分函数的单调区间 。(驻点也称为稳定点,临界点 。拐点在数学上指改变曲线向上或向下方向的点,直观地说拐点是使 。
拐点和极值点的区别?函数的导数为0的点称为函数的驻点,驻点可以划分函数的 。(驻点也称为稳定点,临界点 。) 驻点和拐点的区别 在驻点处的单调性可能改变,在拐点处单调性也可能 。
驻点为什么不一定是极值点?实际上极值点不一定是驻点,而驻点也不一定是极值点, 定义驻点:对于y=f(x),使一阶导数f'(x)=0的点是函数的驻点 。函数极值点不一定是驻点,如f(x)=|x|,在x=0 。
驻点一定是极值吗?如果极值点是可导的点,那么一阶导数一定为0,即可导的极值点一定是驻点 。但是极值点完可以是不可导的点,比方说y=|x|,这个函数,在x=0点处,函数从从单调递减 。
【驻点和极值点的区别】

