欧几里得算法是什么??

欧几里得算法又称辗转相除法 , 是指用于计算两个非负整数a , b的最大公约数 。
应用领域有数学和计算机两个方面,计算公式gcd(a,b) = gcd(b,a mod b) 。
欧几里得算法和扩展欧几里得算法可使用多种编程语言实现 。
算法简介:
欧几里得算法是用来求两个正整数最大公约数的算法 。
古希腊数学家欧几里得在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里得算法 。
扩展欧几里得算法可用于RSA加密等领域 。
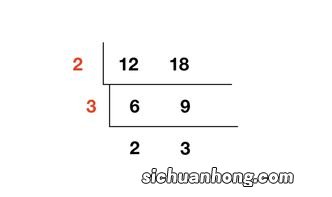
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里得算法,是这样进行的:
1997 / 615 = 3 (余 152)
615 / 152 = 4(余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)
至此,最大公约数为1,以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 1997 和 615 的最大公约数 1 。
以上内容参考 百度百科-欧几里得算法
The Euclidean Algorithm
欧几里德算法(又称辗转相除法)是一种用于快速寻找两个整数的最大公约数的技巧 。
最大公约数 Greatest Common Divisor (GCD):整数 A 和 B 的最大公约数是指能够同时整除 A 和 B 的最大整数 。
使用欧几里德算法寻找 GCD(A,B) 的过程如下:
欧几里德算法使用了下述特性:
如果 A 和 B 其中一个为 0,便可利用前两个特性得出 GCD 。第三个特性帮助我们将大而复杂的问题化简为小而容易解决的问题 。欧几里德算法先利用第三个特性迅速化简问题,直至可以通过前两个特性求解为止 。
证明 GCD(A,0)=A的过程如下:
GCD(0,B)=B的证明过程与此类似,区别仅在于用 B 替换 A 。
先证明较简单的 GCD(A,B)=GCD(B,A-B),再证明 GCD(A,B)=GCD(B,R)
根据定义 GCD(A,B) 可均分 A 。因此,A 一定是 GCD(A,B) 的倍数,即 X?GCD(A,B)=A,此处的 X 是某个整数 。根据定义 GCD(A,B) 可均分 B 。因此,B 一定是 GCD(A,B) 的倍数,即 Y?GCD(A,B)=B , 此处的 Y 是某个整数 。
根据 A-B=C 可得出:
由此可见 GCD(A,B) 可均分 C 。上图的左侧部分展示了此证明,提取如下:
证明 GCD(B,C) 均分 A
根据定义 GCD(B,C) 可均分 B 。因此,B 一定是 GCD(B,C) 的倍数 , 即 M?GCD(B,C)=B ,此处的 M 是某个整数 。根据定义 GCD(B,C) 可均分 C 。因此,C 一定是 GCD(B,C) 的倍数,即 N?GCD(B,C)=B , 此处的 N 是某个整数 。
根据 A-B=C 可得出:
B+C=A
M?GCD(B,C) + N?GCD(B,C) = A
(M + N)?GCD(B,C) = A
由此可见 GCD(B,C) 可均分 A 。下图展示了此证明:
证明 GCD(A,B)=GCD(A,A-B)
根据定 GCD(A,B) 均分 B
同时,已证明 GCD(A,B) 均分 C
因此,GCD(A,B) 是 B 和 C 的公约数
由于 GCD(B,C) 是 B 和 C 的最大公约数,所以 GCD(A,B) 必须小于或等于 GCD(B,C) 。
根据定义 GCD(B,C) 均分 B
同时,已证明 GCD(B,C) 均分 A
因此,GCD(B,C) 是 B 和 A 的公约数
由于 GCD(A,B) 是 A 和 B 的最大公约数,所以 GCD(B,C) 必须小于或等于 GCD(A,B) 。
∵ GCD(A,B)≤GCD(B,C) 且 GCD(B,C)≤GCD(A,B) ∴ GCD(A,B)=GCD(B,C) 即 GCD(A,B)=GCD(B,A-B)
下图的右侧部分展示了此证明的图示:
前面已证明了 GCD(A,B)=GCD(B,A-B) 另外,对于 GCD( ) 而言,括号中各项的顺序并不重要,因此 GCD(A,B)=GCD(A-B,B) 那么,如果反复应用 GCD(A,B)=GCD(A-B,B),便可得到: GCD(A,B)=GCD(A-B,B)=GCD(A-2B,B)=GCD(A-3B,B)=...=GCD(A-Q?B,B) 由于 A= B?Q + R 可得 A-Q?B=R,所以GCD(A,B)=GCD(R,B)。由于括号中各项的顺序并不重要,因此最终可得: GCD(A,B)=GCD(B,R)
找寻 270 和 192 的最大公约数:
A=270, B=192
A=192, B=78
A=78, B=36
A=36, B=6
A=6, B=0
从上面的过程可以看出: ∵ GCD(270,192) = GCD(192,78) = GCD(78,36) = GCD(36,6) = GCD(6,0) = 6 ∴ GCD(270,192) = 6
###其它资料参考###欧几里德算法
欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数 。其计算原理依赖于下面的定理:
定理:gcd(a,b) = gcd(b,a mod b)
证明:a可以表示成a = kb + r,则r = a mod b
假设d是a,b的一个公约数,则有
d|a, d|b,而r = a - kb,因此d|r
因此d是(b,a mod b)的公约数
假设d 是(b,a mod b)的公约数,则
d | b , d |r,但是a = kb +r
因此d也是(a,b)的公约数
因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等,得证 。
欧几里德算法就是根据这个原理来做的,其算法用C++语言描述为:
void swap(int &a, int &b)
{
int c = a
a = b
b = c
}
int gcd(int a,int b)
{
if(0 == a )
{
return b
}
if( 0 == b)
{
return a
}
if(a >b)
{
swap(a,b)
}
int c
for(c = a % b c >0 c = a % b)
{
a = b
b = c
}
return b
}
参考资料:internet
###其它资料参考###欧几里德如下:
欧几里德定理是指射影定律 。
欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数 。其计算原理依赖于下面的定理: 定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0) 证明:a可以表示成a = kb + r,则r = a mod b 假设d是a,b的一个公约数,则有 d|a, d|b,而r = a - kb,因此d|r 因此d也是(b,a mod b)的公约数 因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等 , 得证
直角三角形射影定理,又称“欧几里德定理” , 定理内容是直角三角形中,斜边上的高是两直角边在斜边上射
影的比例中项,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项 。
证明思路
因为射影就是将原图形的长度(三角形中称高)缩放,所以宽度是不变的,又因为平面多边形的面积比=边长的平方比 。所以就是图形的长度(三角形中称高)的比 。
【工商银行一类卡限额是多少】那么这个比值应该是平面所成角的余弦值 。在两平面中作一直角三角形,并使斜边和一直角边垂直于棱(即原多边形图的平面和射影平面的交线),那么三角形的斜边和另一直角边的比值就是其多边形的长度比,即为平面多边形的面积比,而将这个比值放到该平面三角形中去运算即可 。

